$fn – System Variable

This variable is used to set the number of fragments to draw an arc. The CSG ( Constructive Solid Geometry ) used by OpenSCAD, draw circular and spherical objects using line segments and as a result faces.

The$fn determines how many line segments are used, as a result the $fn arguement can be used in multiple ways. The first is create smoother arcs and spherical surfaces. The second is to various regular polygons and solids.

First let’s look at using $fn for the entire model

If we place the $fn=xx; variable at any place in our model the entire model will use that value.

$fn=50;
sphere( 4  );
translate([5,0,0]) cylinder(10,center = true);

will have the same effect as

sphere( 4  );
translate([5,0,0]) cylinder(10,center = true);
$fn=50;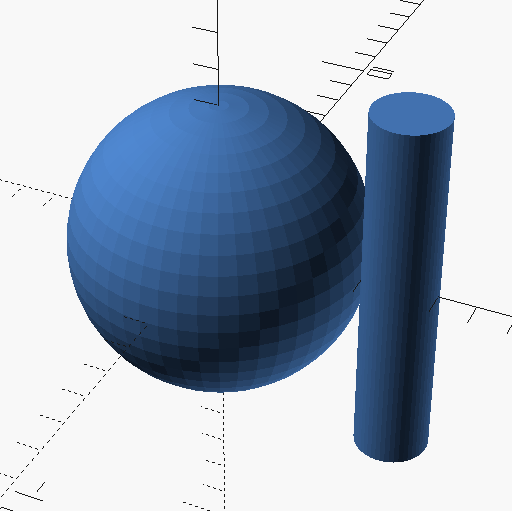

The “global” setting can be overridden “locally”. With the following you can see how the sphere with the same radius can be rendered with different numbers of fragments.

$fn=50;
sphere( 4  );
translate([5,0,0]) cylinder(10,center = true);
translate([10,0,0])sphere(4,$fn=10);

Now let’s examine it’s effects per object.

Being as regular polygons share the same basic elements as a circle, ie radius. We can create any n-sided polygon if all sides are equal.

For example to create a triangle we can use:

circle(3, $fn=3 );

Will result in:

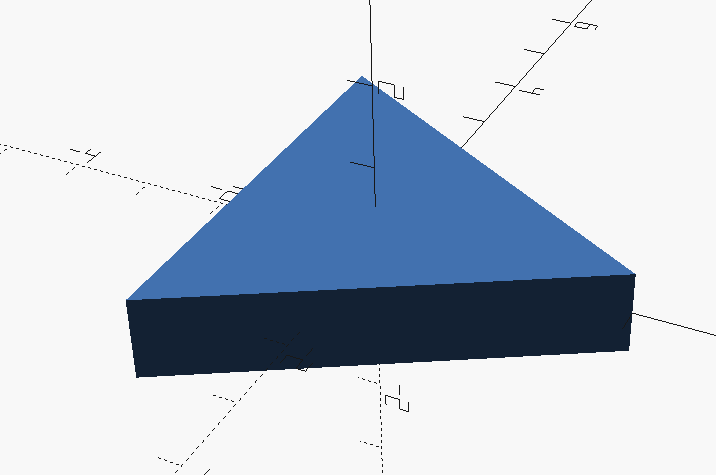
In this example, we have 3 fragments that equate to the sides of the triangle.

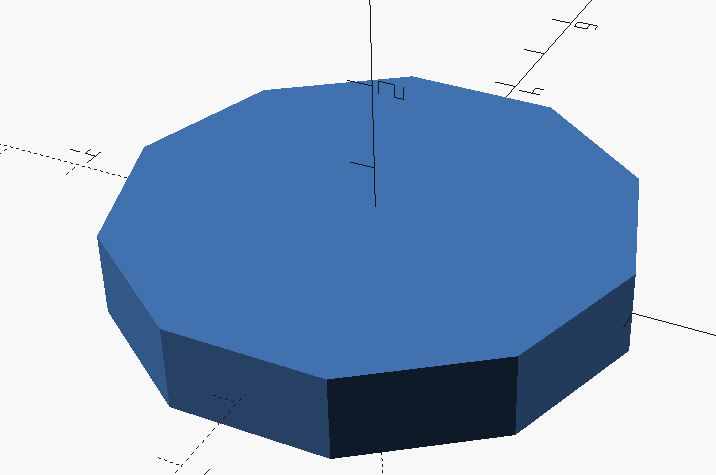
If we wanted to create something more complex say a Regular Decagon:

circle(3, $fn=10);

Notice the only thing that changes was the number of fragements:

We can apply this to 3 Shapes as well. Using 3 for the number of fragments gives us a basic prism.

sphere( 3, $fn=3  );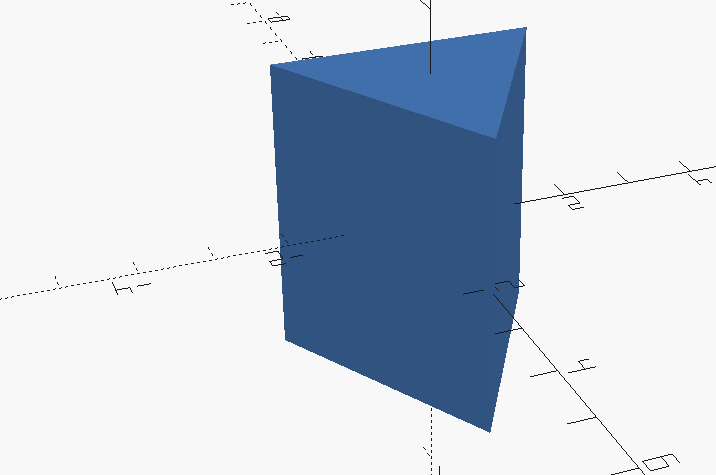

as we increase the fragment numbers we move through the various sided polyhedrons. With just the $fn, we can not produce all the regular polyhedrons.

sphere( 3, $fn=5  );

The fragments are divided evenly around the circumference of the sphere at the XY Plane.